The thing about thinking

When facing a math problem, any problem really, that one is motivated to solve, one thinks about it. Maybe not for long, and often in non-productive ways, but still.

I believe that when many students face math problems, their thinking goes something like this:

1. I can't do this, can I do this? Maybe, but no probably not, or can I...?
2. What should I do? What method should I use? 
3. Where is the example I should copy?
4. It says "triangle" in the question, where are the trig formulas?
5. What should I plug into the formulas?

This approach is almost complete procedure-oriented, and often the student launches into a procedure without even bothering to really understand the question.  I had a student asking for help recently with a question on compound interest, in which someone had first received 4% p.a. interest for 5 years, and then 3.25% p.a. for the next 3 years. This student understood the idea of compound interest, and knew how to calculate how much there would be after 5 years, but "didn't know what number to plug in for the capital for the second investment period." 

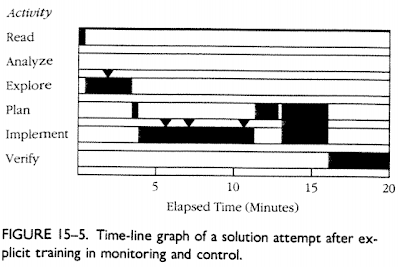
Schoenfield, in this article, shows a time-line of student thinking during a 20 minute mathematical problem solving session. In daily activities such as classwork or homework, I think the student would have given up after 5 minutes. 

While I'd like their thinking to go like this: 

1. What does the question mean? How do I know I understood it correctly? 
2. What mathematical concepts and language represent the type of event that is described in the question?
3. What information do I have? What am I looking for? 
4. So what's the plan: how will I get what I'm looking for?
5. Am I making progress towards a solution, or should I rethink my approach or my understanding of the question?

Schoenfield, presents this timeline of a mathematician solving a problem: 

(each marker "triangle" represents a meta-cognitive observation)

So I'm wondering: why are the students preferring non-productive thinking, and how do I get them to change thinking strategies?

My guess is, most students use non-productive thinking because 

• they don't care enough about mathematical questions to try to understand them
• they feel stressed when facing mathematical questions, and stress is bad for thinking
• they have been rewarded for this type of thinking before, with teachers who provided examples and then "practice" exercises which only required copying examples
• Their teachers and textbooks have exclusively focused on mastery of procedures
• Finally, some students (especially in younger ages) may have cognitive developmental difficulties in understanding abstract mathematical concepts, while copying procedures is possible even for monkeys.

So what's a teacher to do?  Schoenfield suggests the following teaching strategies: 

The good news, according to Schoenfield, is that teaching strategies such as those he lists above can bring about dramatic changes in student thinking.

The bad news, is that in this time-line students are still spending almost no time at all analyzing the situation. They do have more meta-cognitive monitoring, and they seem to be planning the approach, but it seems that the approach is still heavily procedure-driven. 

So maybe just problem solving (with rich problems) and good teaching strategies surrounding problem solving are insufficient tools for changing student thinking in the direction of understanding. Perhaps we need to give them other types of questions altogether, questions that do not require calculation - but rather "simply" understanding. Malcolm Swan's set of five activities for increasing conceptual understanding are excellent for this purpose. He describes them superbly in this document. Above all, I hope that by using activities that ask students to categorize examples, match different representations, and evaluate mathematical statements, students will learn to aim first and foremost for understanding instead of procedure.